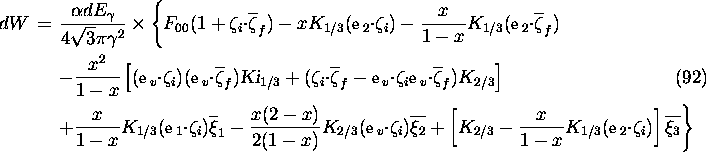
where
Polarization effects have been added since 2.1.
In order to describe polarizations, let us introduce an orthonormal
basis vector (![]() ,
, ![]() ,
, ![]() ).
Here,
).
Here, ![]() is the unit vector
along the initial electron velocity,
is the unit vector
along the initial electron velocity, ![]() the unit vector along
the direction of the transverse component of acceleration, and
the unit vector along
the direction of the transverse component of acceleration, and
![]() .
If the acceleration is due to a transverse magnetic field,
.
If the acceleration is due to a transverse magnetic field,
![]() is the unit vector along the magnetic field (times
the sign of charge).
The transition rate from the initial electron polarization
is the unit vector along the magnetic field (times
the sign of charge).
The transition rate from the initial electron polarization ![]() to the final polarization
to the final polarization ![]() with the photon Stokes parameter
with the photon Stokes parameter ![]() (based on the basis vector (
(based on the basis vector (![]() ,
, ![]() ,
, ![]() ))
is
))
is
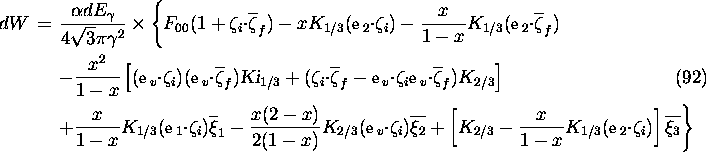
where ![]() is defined in eq.(85) and the argument of the Bessel
functions is z. We omitted the terms involving
is defined in eq.(85) and the argument of the Bessel
functions is z. We omitted the terms involving ![]() and
and ![]() simultaneously, which means to ignore the correlation of polarization
between the final electron and photon.
(See Sec.5.2.2 for the meaning of bars on
simultaneously, which means to ignore the correlation of polarization
between the final electron and photon.
(See Sec.5.2.2 for the meaning of bars on
![]() and
and ![]() .)
.)
The radiation energy spectrum summed over the final polarization is given
by eq.(85) with ![]() replaced by
replaced by
![]()
Since the function ![]() with
with
![]() replaced by
replaced by ![]() has still the above mentioned property,
the same algorithm of generating the photon energy can be used.
(
has still the above mentioned property,
the same algorithm of generating the photon energy can be used.
(![]() is slightly larger when
is slightly larger when ![]() but still
but still ![]() .)
.)
For the given radiation energy ![]() , the polarizations of
the final electron and photon are calculated by the prescription
described in Sec.5.2.2. Thus,
, the polarizations of
the final electron and photon are calculated by the prescription
described in Sec.5.2.2. Thus,
![]()
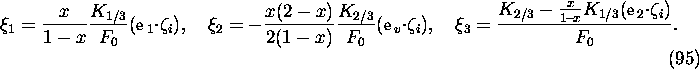
In the case when the event
generation is rejected, the polarization of the electron must be
changed according to eq.(12):
![]()
In storage rings, the electron polarization builds up slowly along the
direction of the magnetic field. This effect comes from the difference
between the coefficient of ![]() and
and ![]() (see eq.(14)):
(see eq.(14)):
![]()
When ![]() is small
(
is small
(![]() in storage rings), each term on the left hand side
is proportional to
in storage rings), each term on the left hand side
is proportional to ![]() whereas the right hand side is
whereas the right hand side is ![]() because of cancellation. CAIN cannot reproduce such slow
buildup, even if the computing time allows, because the approximate polynomials
adopted do not have that accuracy. They are enough, however, for beam-beam
problems.
because of cancellation. CAIN cannot reproduce such slow
buildup, even if the computing time allows, because the approximate polynomials
adopted do not have that accuracy. They are enough, however, for beam-beam
problems.