CAIN functions

    In addition to the predefined functions of general use, such as Sin and Cos, there are other special functions intrinsic to CAIN. There is one limitation on the arguments of the CAIN functions: the arguments must not contain any CAIN functions (due to the problem of FORTRAN recursive call).

  Firstly, the average coordinates and energy-momentum and their r.m.s. values of the beam at the given moment are retrieved by
A vrT, AvrX, AvrY, AvrS, SigT, SigX, SigY, SigS,
A vrEn, AvrPx, AvrPy, AvrPs, SigEn, SigPx, SigPy, SigPs
The calling sequence is common to these 16 functions. Let us take SigX as an example.
S igX(j,k) (j= 1 or 2 or 3, k= 1 or 2 or 3)
returns the horizontal r.m.s. size of right-going (j=1) or left-going (j=2) or both (j=3) of the photon (k=1) or electron (k=2) or positron (k=3) beam. If there is one more argument like
S igX(j,k,)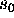
then the particles are restricted to those in the region 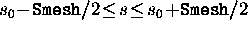. The variable Smesh must be defined before.

  The coordinates and the energy momentum of the test particles can be retrieved by the functions
T estT, TestX, TestY, TestS, TestEn, TestPx, TestPy, TestPs
The calling sequence is, for example, TestX('name') or TestX(n), where 'name' is the character string for the particle name and n is an expression representing an integer 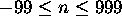. (See Sec.3.3 for the test particle name.)

  There are functions related to the luminosity:
L um, LumH,
L umW, LumWbin, LumWH,
L umEE, LumEEbin, LumEEH
See Sec.3.9 for definitions for these functions.