Since the intensity of synchrotron radiation is on the same order as the beam
itself, it would be very dangerous if they scatter at the pole tips of the nearest
quadrupole magnet; it is also very difficult to shield them near the IP.
The amount of synchrotron radiation is determined by both the size and divergence of
the beam profile, since they are emitted tangentially to the beam envelope.
The beam size shall be well defined by the collimation, while the divergence is given by
the optics(
) and emittance(
) in the final focus system
with the relation 
,
where 
, in order to maximize
the luminosity. Therefore, the amount of synchrotron radiation must be controlled by
collimation. If we can not control it by some means, we must change the optics to enlarge
so that 
decreases. We may thus even have
to sacrifice the luminosity because of 
. A similar situation would likely occur at the
beginning of operation with a larger emittance than the expected one, as happened in the
SLC experiments.
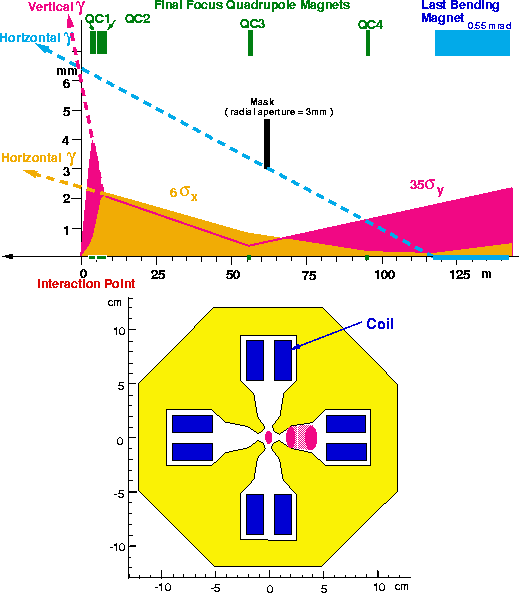
Figure 6: Profiles of the synchrotron radiation at QC1.
The profile at the center accompanies the in-coming beam. The two right-hand
side's ones are passing through QC1 of 2.4m long after a collision with a 8mrad
horizontal crossing.
Figure 5: Horizontal(6
) and vertical(35) beam envelopes through the
last bending magnet and four final focus quadrupole magnets(QC1,QC2,QC3,QC4) for the JLC-I.
The maximum divergences of the synchrotron radiation are also drawn by arrows.
Figure 5 shows beam envelops of 
from the last
bending magnet to the IP(for a distance of 
140m) at JLC-I, where the smearing
effect due to collimation is not taken into account because its probability was
estimated to be very small(
). With a mask of 3mm radial aperture located at 60m
from the IP, synchrotron radiation from the upstream magnets beyond the last bending magnet
can be completely collimated so that they pass through the nearest quadrupole magnet(QC1)
without scattering, since the half aperture of the QC1 is 6.85mm.
As can be clearly seen in Fig.5, the radiations from QC3 and QC2 provide the
maximum divergences at the IP in the horizontal and vertical directions, respectively.
The profiles of the radiation at the QC1 are shown in
Fig.6. The length and inner aperture of the QC1 are 2.4m and 13.7mm
,
respectively, and the front face is located 2.5m from the IP.
The in-coming radiation passes through the central axis of QC1. After a collision with
8mrad horizontal crossing angle, the out-going radiation passes at the off-axis, which is
depicted as two elliptic profiles connecting each other in Fig.6.
As described above, it is expected that there should be no background problems due to the synchrotron radiation if we carefully optimize the collimation and the optics simultaneously.