An enormous amount of ![]() pairs will be created during collisions, for instance a few
times
pairs will be created during collisions, for instance a few
times ![]() pairs per bunch crossing. While their vast majority are scattered
into extremely forward angles, some can be greatly deflected by the strong magnetic field
that is produced by the on-coming beam. In such cases they can enter the detector region and
can create background noise to the detector facility.
pairs per bunch crossing. While their vast majority are scattered
into extremely forward angles, some can be greatly deflected by the strong magnetic field
that is produced by the on-coming beam. In such cases they can enter the detector region and
can create background noise to the detector facility.
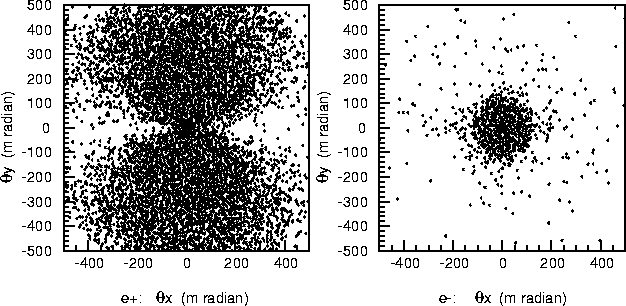
Figure 14.6: Electrons and positrons scattered by beam-beam interaction at IP.
The vertical and horizontal axes denote the scattering angles in the vertical and horizontal
directions, respectively. The left- and right-hand figures show the distributions of the
positrons and electrons, respectively, downstream of the electron beam. Since the
positrons have the same sign charge as the in-coming (positron) beam, they are scattered
by larger angles than the electrons.
Figure 14.6 shows the angular distributions of pair-produced electrons and
positrons after the beam-beam interaction. The calculation was made using
ABEL[7]. Many particles (electrons or positrons) are scattered at large angles
exceeding 200 mrad. We can also clearly see an asymmetry in their azimuthal
distribution. More particles are deflected in the vertical direction than in the horizontal
because of a very flat transverse beam profile (![]() ). Since the energies of the particles are relatively small,
and are at a few hundreds MeV, most of these particles are confined near to the beam axis due
to the detector solenoid magnetic field of 2 T. However, when they hit QC1 in the out-going
side, many secondary photons are back-scattered uniformly into the detector region. They
can become serious background.
). Since the energies of the particles are relatively small,
and are at a few hundreds MeV, most of these particles are confined near to the beam axis due
to the detector solenoid magnetic field of 2 T. However, when they hit QC1 in the out-going
side, many secondary photons are back-scattered uniformly into the detector region. They
can become serious background.
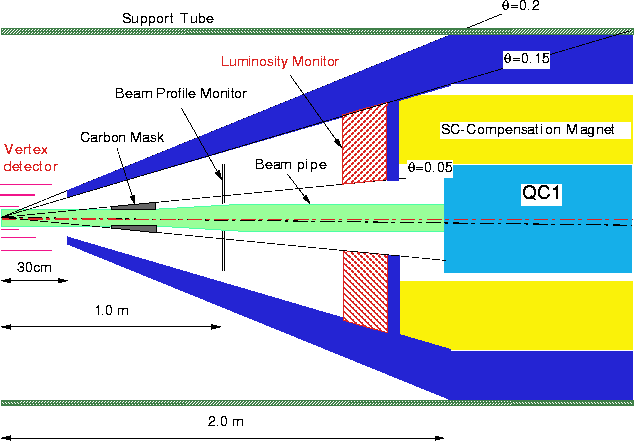
Figure 14.7: Schematic view of the interaction region for ![]() 0.5TeV.
0.5TeV.
A possible configuration of the interaction region is shown in Figure 14.7. A
cone-shaped mask of heavy metal (tungsten) will be used to absorb the photons with good
efficiency. The mask occupies a polar angle region of 0.15![]() 0.2 .
The front aperture of the mask needs to be minimized in the light of reducing the
background. However, it has to let the core part of the incoming beam pass through. An
aperture size of r=4.5 cm was chosen. The conical mask is mechanically connected to a
10.36 cm-thick cylindrical mask of the same material in a hermetic manner.
A doublet of the final focus quadrupole magnets, QC1 and QC2, is implemented
inside the mask. QC1 and QC2 are surrounded by a super-conducting solenoid magnet that
compensates for the detector solenoid field of 2 T.
0.2 .
The front aperture of the mask needs to be minimized in the light of reducing the
background. However, it has to let the core part of the incoming beam pass through. An
aperture size of r=4.5 cm was chosen. The conical mask is mechanically connected to a
10.36 cm-thick cylindrical mask of the same material in a hermetic manner.
A doublet of the final focus quadrupole magnets, QC1 and QC2, is implemented
inside the mask. QC1 and QC2 are surrounded by a super-conducting solenoid magnet that
compensates for the detector solenoid field of 2 T.
A detailed engineering design of the compensating magnet is not yet complete. However,
naturally, a sufficient space needs to be allocated to accommodate these magnets inside the
mask. In addition, inside the conical mask, two kinds of detectors will be installed: a beam
profile monitor (at 1 m from the IP, to be described in the next section), and a luminosity
monitor of tungsten-scintillator sandwich type (at 1.63 m from the IP, covering ![]() ). A set of 20 cm-thick carbon masks is also implemented (0.5 m from the
IP). The carbon mask is designed to absorb back-scattered low energy particles. The mask
will be built as an ``active" device, which generates signals to veto scattered
electrons/positrons at
). A set of 20 cm-thick carbon masks is also implemented (0.5 m from the
IP). The carbon mask is designed to absorb back-scattered low energy particles. The mask
will be built as an ``active" device, which generates signals to veto scattered
electrons/positrons at ![]() 0.05 in combination with with the luminosity monitor. They
are considered to be important detector elements for studies of SUSY physics[3].
0.05 in combination with with the luminosity monitor. They
are considered to be important detector elements for studies of SUSY physics[3].
In order to estimate the background due to low-energy electron-positron pairs in the detector, numerical simulations have been conducted. The pairs, which are generated by the ABEL code, were tracked by employing a Monte Carlo program based on GEANT3.21[8]. This simulation software is called JIM (Jlc detector sIMulator). JIM takes account of the geometries of all the detectors, which have been described in the JLC-I[1], except for a few small revisions: The vertex detector is now assumed to have 3 layers instead of 2 as stated in JLC-I. The inner radius of the central drift chamber has been increased from 30 cm to 45 cm. Also the arrangement of the final focus quadrupole magnets(QC1 and QC2) and the masks follow the geometry shown in Figure 14.7.
For an accurate estimation of the background in the detectors, the threshold energies of the
electrons/positrons and photons, i.e. the minimum energies to be tracked in JIM,
have been set fairly low at 200 KeV and 10 KeV, respectively. The simulated statistics
presented here corresponds to 10 bunch-crossings. The beam parameters used in this
simulation were taken from the standard ![]() 500GeV operation. The values of the major
parameters are:
500GeV operation. The values of the major
parameters are: ![]() e's/bunch, 85 bunches/train, a repetition rate of 150Hz,
e's/bunch, 85 bunches/train, a repetition rate of 150Hz,
![]() nm and a horizontal crossing angle of
nm and a horizontal crossing angle of ![]() mrad. This
corresponds to a luminosity of
mrad. This
corresponds to a luminosity of ![]() cm
cm![]() s
s![]() with a crab
crossing. In this simulation the crab crossing was assumed to be perfect so that two
beams collide head-on.
with a crab
crossing. In this simulation the crab crossing was assumed to be perfect so that two
beams collide head-on.
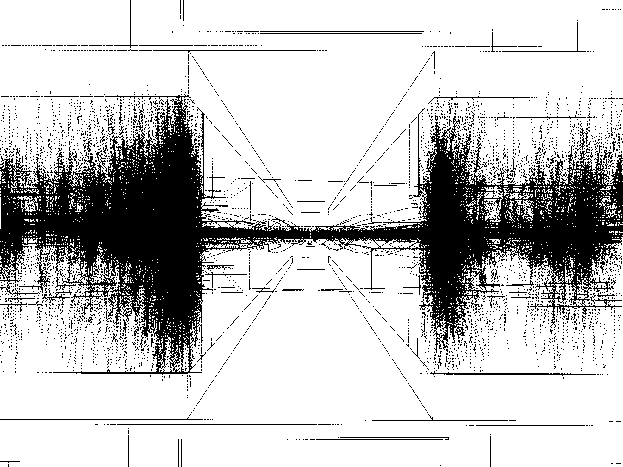
Figure 14.8: Particles of ![]() pairs simulated by JIM based on GEANT3, where the
solid and dotted lines are electrons/positrons and photons, respectively. The statistics
corresponds to 1/100 of a bunch crossing for a display purpose.
pairs simulated by JIM based on GEANT3, where the
solid and dotted lines are electrons/positrons and photons, respectively. The statistics
corresponds to 1/100 of a bunch crossing for a display purpose.
Figure 14.8 shows the pairs and secondary (back-scattered) particles simulated
with the JIM code. As can be clearly seen in the figure, most of them, appearing like the core
of dark band in the figure, pass through the front aperture (R![]() =4.5cm) of the mask.
Particles outside of the core are scattered by much larger angles than the deflected
ones, which represent a possible background to be considered.
=4.5cm) of the mask.
Particles outside of the core are scattered by much larger angles than the deflected
ones, which represent a possible background to be considered.
The number of hits detected in the detectors is plotted as a function of the radial distance in
Figure 14.9. The number of tracks that create those hits is similarly
plotted in Figure 14.10. In these figures, the contributions from
secondary particles are also plotted by solid circles. Here, the secondary particles are
simply defined as those having off-vertex positions, i.e. ![]() mm or
mm or ![]() mm.
mm.
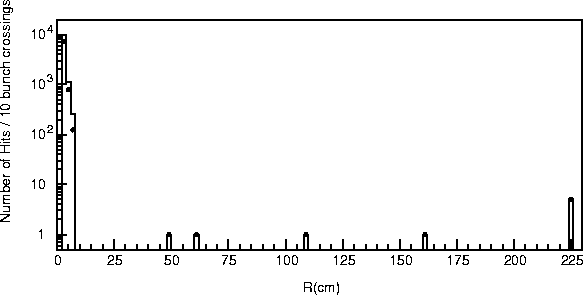
Figure 14.9: Number of hits detected in the detectors as a function of the
radial distance for 10 bunch-crossings, where those produced by secondary particles are
indicated by solid circles.
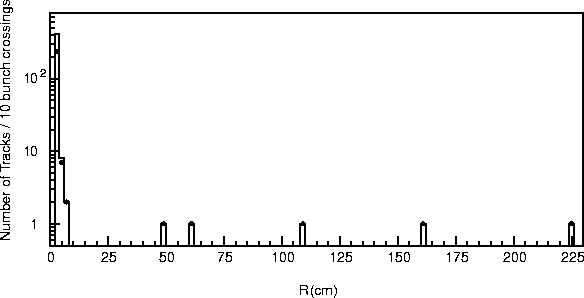
Figure 14.10: Number of tracks creating the hits in the previous figure as a function of
the radial distance for 10 bunch-crossings, where those produced by secondary particles are
also indicated by solid circles.
We note here that the vertex detector consists of ![]() m
m![]() pixels (CCDs), and
that three layers are located at r=2.5(z=
pixels (CCDs), and
that three layers are located at r=2.5(z=![]() cm), 5.0(z=
cm), 5.0(z=![]() cm) and 7.5cm(z=
cm) and 7.5cm(z=![]() cm). With these geometry parameters the hit densities were calculated to be 3.6, 0.1 and
0.01 hits/mm
cm). With these geometry parameters the hit densities were calculated to be 3.6, 0.1 and
0.01 hits/mm![]() for one machine pulse consisting of 85 bunch crossings (at 150Hz),
respectively. We have assumed here that the hits are distributed uniformly within each
layer. It should be noted, however, that since the actual angular distribution of pair
particles is asymmetric, as shown in Figure 14.11, the hit counts quoted here
represent only the average numbers.
for one machine pulse consisting of 85 bunch crossings (at 150Hz),
respectively. We have assumed here that the hits are distributed uniformly within each
layer. It should be noted, however, that since the actual angular distribution of pair
particles is asymmetric, as shown in Figure 14.11, the hit counts quoted here
represent only the average numbers.
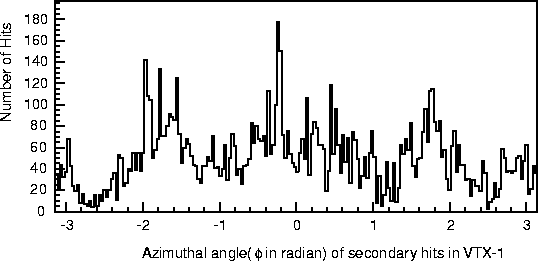
Figure 14.11: Angular distribution of hits on the first layer of the vertex detector for 10
bunch-crossings.
On the average, a single charged particle track originating from the pair creation
process will produce about 20 hits on the first layer of the vertex detector. This number is
arrived at by comparing figures 14.9 and 14.10. Except
for the first layer, the hit rates in the vertex detector are well below 1 hit/mm![]() , which
is considered an empirical limit[9, 6].
, which
is considered an empirical limit[9, 6].
About a half of the hits in the first layer, as shown in Figure 14.9, are due to secondary particles. Contrary to our first expectation, the carbon mask was found to have no significant effect on the first layer background rate, while some reduction of hits was seen in the second layer. Figure14.12 shows transverse vertex positions (x ,y) for z>1.6 m of the secondary particles observed in the first layer. It should be recalled that this first layer can clearly see the pole tips of QC1. In fact, this may explain why the existence of the carbon mask did not quite help reduce the low-energy pair background on the first layer.
It is considered that more simulation studies and optimizations of the relative geometry
of carbon masks are necessary. Also, a more detailed calculation of particle tracking with the
vertex detector may reveal that for the first layer a background hit rate in excess
of 1 hit/mm![]() is actually acceptable. This study should be also pursued.
is actually acceptable. This study should be also pursued.
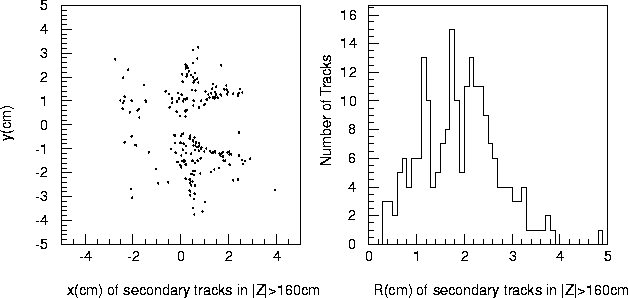
Figure 14.12: Transverse distribution of secondary particles at z >1.6m for 10
bunch-crossings.
In the central tracking region of r > 45cm, we expect about one hundred hits machine pulse
(85 bunches per pulse at 150 Hz) as shown in Figure 14.9. This hit rate
corresponds to ![]() % occupancy in the tracking chamber. Since most of these hits
are created by back-scattered photons, they are uniformly distributed in the tracking
volume. Also their hit pattern is such that they rarely form contiguous hits
that can be misidentified as charged particle tracks that originate from the IP.
Therefore, no significant background problems from the pairs are expected in this region.
% occupancy in the tracking chamber. Since most of these hits
are created by back-scattered photons, they are uniformly distributed in the tracking
volume. Also their hit pattern is such that they rarely form contiguous hits
that can be misidentified as charged particle tracks that originate from the IP.
Therefore, no significant background problems from the pairs are expected in this region.