



Next: muon background
Up: Collimation
Previous: material
K.Yokoya derived a theoretical expression of wakefield induced by the
collimators, which shall be compared to a measurement.
The emittance growth due to the wakefield is expressed by,
| ![\begin{displaymath}
\Delta \varepsilon_y = ( {\Delta y^2 \over{\beta_y}} ) \cdot...
...2}} + {L
\over{a^3}})
+ 0.69 {\theta \over{a \sigma_z}}\biggr]\end{displaymath}](img12.gif) |
(3) |
where 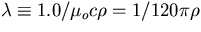 is the resistive
depth of material of the collimator, and
is the resistive
depth of material of the collimator, and 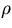 is the conductivity, and N,
is the conductivity, and N,
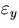 ,
, 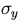 ,
, 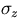 are the intensity/bunch, (vertical)
invariant emittance, vertical beam size, bunch length of the beam,
respectively. re is the electron classical radius. The geometrical
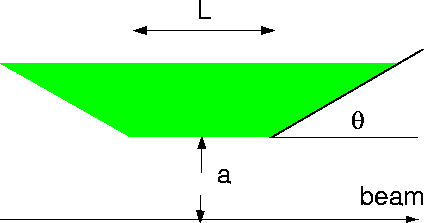
parameters of the collimator are displayed in Fig.3.
are the intensity/bunch, (vertical)
invariant emittance, vertical beam size, bunch length of the beam,
respectively. re is the electron classical radius. The geometrical
parameters of the collimator are displayed in Fig.3.
Figure 3:
Geometry of a collimator.
 |
There is the optimal angle (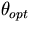 ) minimizing the
) minimizing the 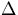 , that is,
, that is,
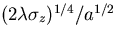 . With this angle and
. With this angle and 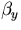 instead of
instead of 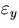 and
and 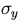 , the
, the 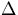 is,
is,
| ![\begin{displaymath}
\Delta = 1.77 N r_e {\beta_y \over{\gamma}}
\biggl[ \sqrt{\l...
...\over{a^3}}
+ \sqrt{2} {\theta_{opt} \over{a \sigma_z}} \biggr]\end{displaymath}](img22.gif) |
(4) |
where 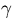 is the Lorentz factor, Ebeam /me.
is the Lorentz factor, Ebeam /me.
The emittance growth should be less than 1% so that the total growth due to 6
collimators is less than 6%. Assuming that the surface of the collimator is
plated by copper, the aperture (a) of the collimator must be 250
(204)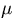 m corresponding to 70.4 (56.9)
m corresponding to 70.4 (56.9) 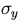 with the length of 20
(10)cm, N = 1010/bunch
with the length of 20
(10)cm, N = 1010/bunch 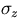 =80
=80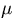 m and
m and 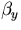 =400m at
Ebeam=750GeV, where the optimal angle (
=400m at
Ebeam=750GeV, where the optimal angle (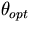 ) is 1.05o
(1.17o) .
) is 1.05o
(1.17o) .




Next: muon background
Up: Collimation
Previous: material
Toshiaki Tauchi
12/20/1999
![\begin{displaymath}
\Delta \varepsilon_y = ( {\Delta y^2 \over{\beta_y}} ) \cdot...
...2}} + {L
\over{a^3}})
+ 0.69 {\theta \over{a \sigma_z}}\biggr]\end{displaymath}](img12.gif)
![\begin{displaymath}
\Delta \varepsilon_y = ( {\Delta y^2 \over{\beta_y}} ) \cdot...
...2}} + {L
\over{a^3}})
+ 0.69 {\theta \over{a \sigma_z}}\biggr]\end{displaymath}](img12.gif)
![\begin{displaymath}
\Delta = 1.77 N r_e {\beta_y \over{\gamma}}
\biggl[ \sqrt{\l...
...\over{a^3}}
+ \sqrt{2} {\theta_{opt} \over{a \sigma_z}} \biggr]\end{displaymath}](img22.gif)
![]() m corresponding to 70.4 (56.9)
m corresponding to 70.4 (56.9) ![]() with the length of 20
(10)cm, N = 1010/bunch
with the length of 20
(10)cm, N = 1010/bunch ![]() =80
=80![]() m and
m and ![]() =400m at
Ebeam=750GeV, where the optimal angle (
=400m at
Ebeam=750GeV, where the optimal angle (![]() ) is 1.05o
(1.17o) .
) is 1.05o
(1.17o) .