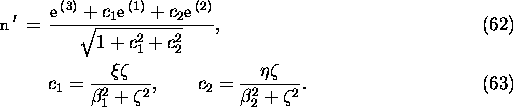
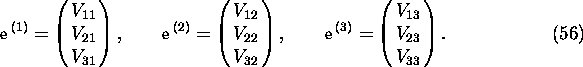
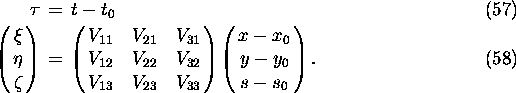
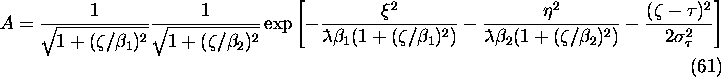
The wave front is given by the contour of ![]() . If one
defines
. If one
defines ![]() by
by ![]() ,
, ![]() is nearly a unit vector and approximated by
is nearly a unit vector and approximated by
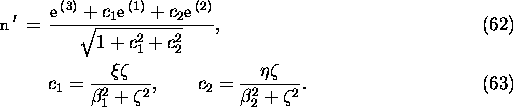
In CAIN, when the relevant particle is at (t,x,y,s), or
at ![]() in laser coordinate, the laser
field is considered to be locally a plane wave with the
power density
in laser coordinate, the laser
field is considered to be locally a plane wave with the
power density ![]() , wave number
k, and the propagation direction
, wave number
k, and the propagation direction ![]() .
.
There is some problem on the polarization because eq.(60)
does not exactly satisfy the Maxwell equation. For simplicity,
the basis ![]()
![]() for
polarization is defined in the following manner:
for
polarization is defined in the following manner: ![]() is the unit vector along
is the unit vector along
![]() and
and
![]() . (This is irrelevant if only
the longitudinal polarization is needed.)
. (This is irrelevant if only
the longitudinal polarization is needed.)
The Lorentz transformation is a little complicated because
eq.(60) is far from a covariant form. The particle coordinates
and the external fields are transformed immediately when LORENTZ
command is invoked and the transformation parameters are
forgotten. In the case of lasers, the transformation is not done
immediately but instead the transformation parameters are stored.
When the laser is called at every time step for each particle,
the particle coordinates are Lorentz transformed back to the
frame where the laser was defined, and the calculated parameters
(A, ![]() ,
, ![]() )
are transformed to the current Lorentz frame. Therefore, the
Lorentz transformation is a little time-consuming.
)
are transformed to the current Lorentz frame. Therefore, the
Lorentz transformation is a little time-consuming.