where
with
Then, the solution is
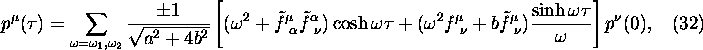
where the upper (lower) sign applies to
The present version of CAIN accepts a constant external field only.
The covariant form of the equation of motion
![]()
where ![]() is the proper time and
is the proper time and ![]() the electromagnetic
field tensor, can be solved exactly when the field is constant.
The eigenvalues of the matrix
the electromagnetic
field tensor, can be solved exactly when the field is constant.
The eigenvalues of the matrix
![]() is given by
is given by ![]() and
and
![]() , where
, where
![]()
with
![]()
Then, the solution is
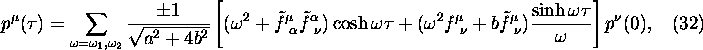
where the upper (lower) sign applies to ![]() (
(![]() )
and
)
and ![]() with
with ![]() being the antisymmetric tensor of
rank 4.
being the antisymmetric tensor of
rank 4.
The classical spin motion of electrons is given by the Thomas-BMT
equation
![]()
where a is the coefficient of
anomalous magnetic moment and
![]()
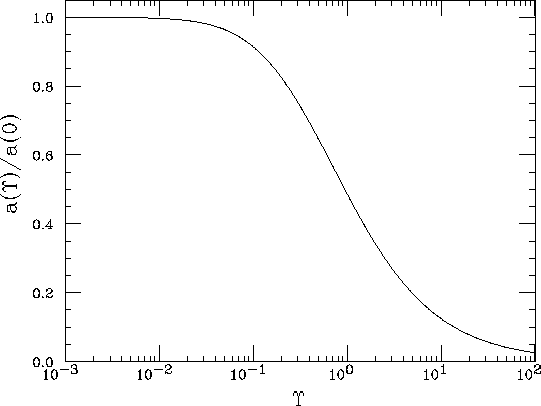
Figure 1: Field dependence of the anomalous magnetic
moment of electron
When the field is very strong, a is different from the well-known
value ![]() but is a function of the field strength
characterized the parameter
but is a function of the field strength
characterized the parameter ![]() .
.
![]()
The functional form of ![]() is shown in Fig.1.
Simple polynomial approximations are used in CAIN.
is shown in Fig.1.
Simple polynomial approximations are used in CAIN.