In future 
linear colliders it is essential to have very
flat beams at the interaction point (IP) in order to obtain high
luminosity. The typical beam size is 3nm(
) x
260nm(
) at IP for the Japan Linear Collider
(JLC-I)[1]. A measurement of the beam size is extremely
important from the view point of beam diagnostics, especially to
maintain the stable operation of linear colliders[2].
Although several ideas have been presented for this purpose, none of
them can be used at IP. Recently, T.Shintake has proposed a nanometer
beam-size monitor utilizing backward Compton scattering of
interfering laser light, which can be used to measure the beam size
down to 5nm[3]. We can not measure with certainty 3nm or
smaller size, even with this method. So far, there has been no idea
of how to clearly measure such a small beam size, much less to
measure it during a collision.
In this paper we describe a completely new idea for measuring the
beam size at IP. As is well known, many low-energy pairs
are expected to be created during beam crossing due to three
incoherent processes: the Breit-Wheeler (BW:
) process, the Bethe-Heitler (BH: 
) process and the Landau-Lifshitz (LL: 
) process, where 
is a
beamstrahlung photon. These phenomena have been investigated as
troublesome background for experiments at future linear
colliders[4]. The particles of our concern have the same
charge as that of the oncoming beam, and are hereafter called
``same-charge" particles. Most of them are deflected at larger
angles than their inherent scattering angles by a strong
electromagnetic force due to the oncoming beam, while the
``opposite-charge" particles must oscillate inside the oncoming beam
because of a focussing force between them; they are deflected with
small angles. Figure 1 shows a schematic view of these
phenomena.
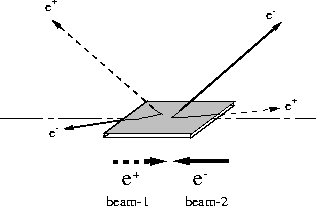
Figure 1:
Schematic view of pair creations and deflections
during a collision, where two flat beams are depicted as overlapping
sheets at IP and two 
pairs are created in forward and
backward angles, only as an example.
They can be well described by a scattering process of 
in
a two-dimensional Coulomb potential which is Lorentz-boosted to the
rest frame of the oncoming beam[5]. Since this potential is
produced by the intense electric charge of the oncoming beam, it is a
function of the transverse size (,) and
intensity of the beam. Therefore, the deflected particles should carry
this information, especially in their angular distribution, which we
intend to measure. It should be noted that we can measure the sizes
of the two beams independently, since the particles must be deflected
asymmetrically in the forward and backward angular regions if the two
beams have different beam parameters, i.e. there are two independent
Coulomb potentials of the two beams separated by a large
Lorentz-boost along the beam axis. Moreover, we can measure the
relative displacement and transverse rotation of two beams. In
addition, this measurement will provide a real-time, fast feedback to
collider-machine operation at the same time that experiments are
being conducted.
In subsequent sections we describe an analytic expression for the angular distribution of elliptic beams, where the charge density is uniform inside an elliptic cylinder, since only this case can be calculated analytically, and, further, it explains most of the features for Gaussian beams under the beam-beam effects at IP. We then present the results of a simulation using the ABEL program[6, 4], which takes account of all known beam-beam effects, for the case of JLC-I as an example of future linear colliders.