In this section we discuss the production of muons through the interaction of particles in the beam tails when they are collimated at the upstream collimation sections.
Generally, the transverse profile of the beam does not exactly follow a Gaussian
distribution at linear colliders. The beams can be accompanied by long tails according to
experience from experiments at SLC [4]. While the origin of these tails is not
thoroughly understood at present, we shall conservatively assume that the beam has a flat
tail beyond ![]() in both the horizontal(x) and vertical(y) directions with
a relative intensity of 1%.
in both the horizontal(x) and vertical(y) directions with
a relative intensity of 1%.
As can be seen in the next section, the beam must be collimated within ![]() and
and ![]() in order to keep the background due to synchrotron radiation at a
manageable level. Since the typical size of the beam core is on the order of a few
in order to keep the background due to synchrotron radiation at a
manageable level. Since the typical size of the beam core is on the order of a few ![]() m,
collimating such beams is a seriously non-trivial task. A work-around is to expand only the
tail part sufficiently by using a non-linear collimation technique, as discussed in Chapter
13. This is part of the reason why a 1200 m-long collimator section is required for
collimating a 0.75 TeV beam.
m,
collimating such beams is a seriously non-trivial task. A work-around is to expand only the
tail part sufficiently by using a non-linear collimation technique, as discussed in Chapter
13. This is part of the reason why a 1200 m-long collimator section is required for
collimating a 0.75 TeV beam.
As stated in Chapter 2 and subsequent chapters, one RF pulse will accelerate a bunch train
which contains up to 85 bunches separated by 1.4 nsec at a repetition rate of 150Hz.
Since each bunch consists of ![]() electrons (or positrons) at the IP, about
electrons (or positrons) at the IP, about
![]() (1%tail)
(1%tail)![]() (bunches) electrons may hit collimators at 150 Hz. In the
interactions of the beam tails with the collimators a large number of muons are produced
through the Bethe-Heitler process,
(bunches) electrons may hit collimators at 150 Hz. In the
interactions of the beam tails with the collimators a large number of muons are produced
through the Bethe-Heitler process, ![]() . Without
suitable measures these muons would traverse through the tunnel and create a large amount
energy deposit within the detector facility. They would cause serious background problems for
conducting high-energy physics experiments.
. Without
suitable measures these muons would traverse through the tunnel and create a large amount
energy deposit within the detector facility. They would cause serious background problems for
conducting high-energy physics experiments.
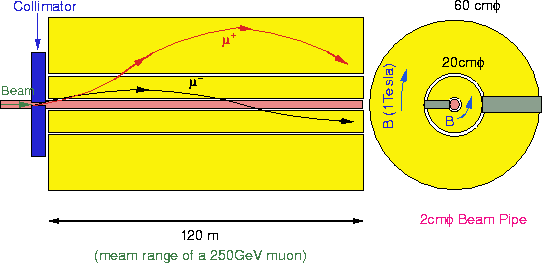
Figure 14.2: Original idea of a muon attenuator. Two iron pipes are
magnetized axially in opposite directions for both charged muons, which can be trapped,
where the 120m length of the iron pipe corresponds to a mean range of 250GeV muons.
Several techniques have been invented so far to reduce the muon background at linear colliders. The first is the ``muon spoiler" idea, which was implemented at SLC. There, a set of large iron toroid magnets are installed in the beam line to over-focus the muons, so that they are dispersed away from the detector.
In the design study here, another method, which is called ``muon attenuator", is considered.
This idea was first proposed by by E.A.Kushnirenko [5]. The principle idea is
to confine ![]() and
and ![]() inside two iron pipes magnetized axially in opposite
directions, and to absorb the muons by the energy loss. A schematic diagram of this scheme
is shown in Figure 14.2. We have performed a simulation study on the attenuation
of muon flux onto the detector when this technique is applied. In the present JLC design there
are six collimators in the collimation section between 1840 m and 2856 m, as measured from the
IP. Various effects of long iron pipe shield of the attenuator was investigated with and
without magnetization. The best condition was found to be the case with no magnetization in
the iron pipes.
inside two iron pipes magnetized axially in opposite
directions, and to absorb the muons by the energy loss. A schematic diagram of this scheme
is shown in Figure 14.2. We have performed a simulation study on the attenuation
of muon flux onto the detector when this technique is applied. In the present JLC design there
are six collimators in the collimation section between 1840 m and 2856 m, as measured from the
IP. Various effects of long iron pipe shield of the attenuator was investigated with and
without magnetization. The best condition was found to be the case with no magnetization in
the iron pipes.
The outer and inner radius of the iron pipe shield are 31 and 1 cm, respectively. The beam
pipe is located inside the iron pipes. The beam line between 1721 m to 2856 m from the IP
except for the collimators is assumed to be covered with the iron shield. Muons that
penetrate through the collimation section are bent by the big bend (+7 mrad, see
Figure 14.1) and go through the tunnel of 3.5 m![]() . In this study a second
bending magnet(-3.28 mrad) is assumed to be located at 80 m from the IP. This is so to
make the horizontal beam crossing, although the actual design has several bending magnets
distributed in the final focus system. Sand stone is assumed to surround the tunnel. The
cross section of the tunnel is shown in Figure 4.78 of Ref.[1].
. In this study a second
bending magnet(-3.28 mrad) is assumed to be located at 80 m from the IP. This is so to
make the horizontal beam crossing, although the actual design has several bending magnets
distributed in the final focus system. Sand stone is assumed to surround the tunnel. The
cross section of the tunnel is shown in Figure 4.78 of Ref.[1].
Figure 14.3 shows the result of the simulation. The horizontal axis gives the
locations of collimators, as measured from the IP in meters. They correspond to the origins
of muons. The vertical axis gives the number of electrons that are required to hit the
collimators so that one muon produced out of these would to hit a detector of
![]() m
m![]() volume size.
volume size.
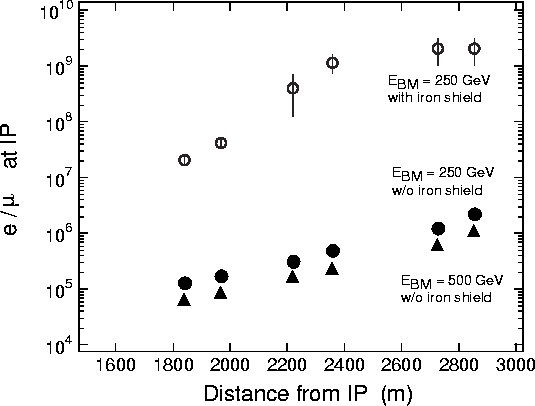
Figure 14.3:
Number of electrons to produce one muon which reaches the IP.
The solid circle, solid triangle and open circle symbols correspond to cases of the beam energies of 250 GeV without the iron shield, 500 GeV without the shield and 250 GeV with the shield, respectively. The result of the simulation can be summarized as below: