In the past, an empirical formula used to describe the distribution of the collision energy at
next-generation linear colliders has been presented by Yokoya and Chen[14].
In addition, recently developed software, called CAIN[13], is capable of simulating
detailed beam-beam interactions at ![]() ,
, ![]() and
and ![]() linear colliders.
The function in [14] has been found to give a good approximation to the CAIN
calculation, as shown in Figure 14.17 at
linear colliders.
The function in [14] has been found to give a good approximation to the CAIN
calculation, as shown in Figure 14.17 at ![]() =250GeV. Table 14.1
summarizes the relevant parameters for the calculations.
=250GeV. Table 14.1
summarizes the relevant parameters for the calculations.
Figure 14.17 shows that the function reasonably reproduce the CAIN result at ![]() GeV, where a small difference seen in the figure is due to a beam disruption
included in the CAIN.
GeV, where a small difference seen in the figure is due to a beam disruption
included in the CAIN.
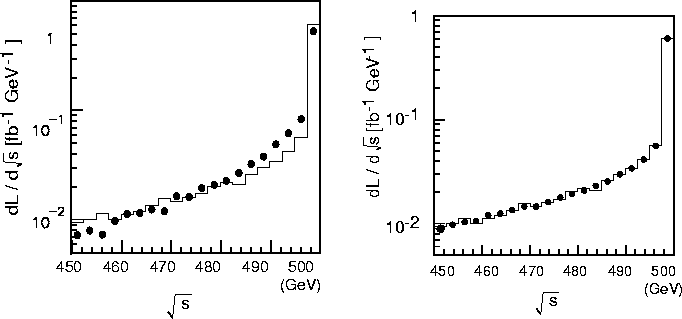
Figure 14.18: Luminosity spectra calculated by the generator (histogram)
and the function (solid circles).
Figure 14.17: Luminosity spectra calculated by the empirical function (histogram)
and CAIN (solid circles).

Table 14.1: Major parameters of JLC.
To improve the efficiency of calculations, a luminosity-spectrum generator code has been created[15]. The generator code precisely reproduces the empirical function as shown in Figure 14.18.
It should be noted that besides the beam-beam interactions, the beam-energy spread also
affects the luminosity-spectrum. Its effects were simulated, and the results are shown in
Figure 14.19. In these calculations a uniform energy spread of ![]() 1% was assumed
for the original beams. It can be seen that the luminosity peaks are smeared at around
1% was assumed
for the original beams. It can be seen that the luminosity peaks are smeared at around
![]() =500GeV.
=500GeV.
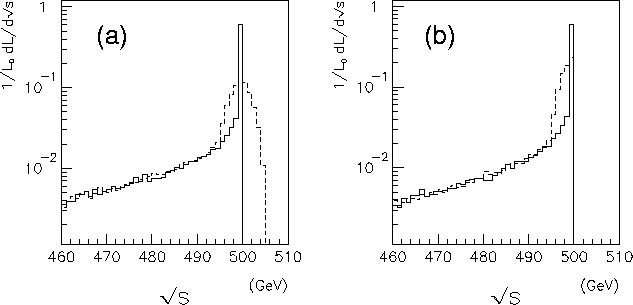
Figure 14.19:
(a) The luminosity-spectra weighted by the Bhabha cross section, without (with) the ![]() 1%
uniform beam-energy spread, which is shown by the solid (dashed) histogram.
(b) The spectra calculated by the acollinearity angles of the Bhabha
events, where no entry above
1%
uniform beam-energy spread, which is shown by the solid (dashed) histogram.
(b) The spectra calculated by the acollinearity angles of the Bhabha
events, where no entry above ![]() =500GeV exists by definition.
=500GeV exists by definition.
The differential cross section of the Bhabha scattering process was calculated using the program GRACE[16]. This is a program package for automatic amplitude calculations. The numerical integration and unweighted event generation were performed by two programs, BASES and SPRING[17], respectively. In this study, the lowest order Feynman diagrams of this process were taken into account, since the effect of the initial state radiation can be precisely estimated[18].