ここでは、JLC トップ サブグループの活動に関して紹介します。
このホームページは、現在開発中です。まだまだ不十分な所ばかりですが、
これからおいおい充実させていくつもりです。
内容に関する御意見をお待ちしています。
コメント等ありましたら、
fujiik@jlcuxf.kek.jp
迄メール下さるようお願いします。
English version of JLC Top Subgroup Home Page is here.
新着情報
新着情報トップ サブ
グループの紹介サブグループでは、理論面、実験面の両方から、 いろいろな人が幅広い活動をしています。 ここではそのごく一部だけを挙げます。
質量が 150 GeV を越える重いトップクォークは大きな崩壊巾を持っている。
m_t (GeV) Gamma_t (GeV)
-----------------------------
100 0.09
125 0.37
150 0.81
175 1.42
200 2.23
-----------------------------
この大きな崩壊巾は、トップ・クォークを他のクォークにない特徴的な物にしている。
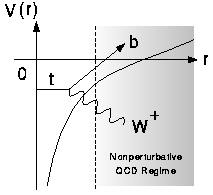
この大きな崩壊巾により原点で生成されたトップ・反トップ対は QCD の非摂動領域に到達する前に崩壊する。
そのおかげで、Fadin と Khoze により最初に指摘されたように、
トップ・反トップ対の生成断面積の摂動 QCD による信頼できる評価が出来る。
こうして、摂動 QCD の明快な検証や、強い相互作用の結合定数 (alpha_s) の精密測定が可能となる。
さらに重要なことは、QCD の寄与が不定性無く計算できることによって、他のより小さい効果（例えばヒッグス交換の寄与）を引き出す可能性が開けたことである。
最も大きな QCD の寄与は、クーロン的なグルーオンの多重交換から来る。 これは、しきい値領域ではトップ・反トップ対はゆっくり走るので、比較的長い間、お互いに近くにいるためである。
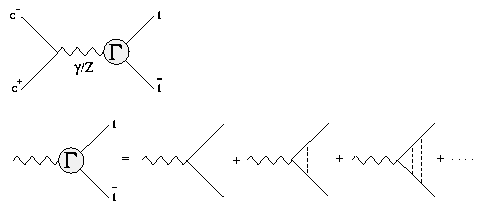
図中で Gamma はしきい値補正因子で、Bethe-Salpeter 方程式を満足する。 この方程式は、非相対論近似で次の Schroedinger 方程式に帰着する。
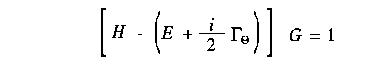
ここで、演算子 G はしきい値補正因子 Gamma と次の関係で結ばれている。 つまり、S-波に対応するベクトル部分については
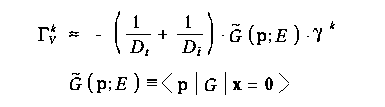
また、P-波に対応する軸性ベクトル部分については
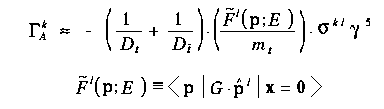
である。
本質的に、しきい値領域でのトップ・反トップ対生成の物理の全てがこの補正因子 Gamma あるいは G に含まれていると言って良い。 Gamma あるいは G は、トップの運動量 (P)、 しきい値から測った重心系エネルギー (E)、 強い相互作用の結合定数 (alpha_s)、 トップの崩壊巾 (Gamma_t)、 そして、ヒッグス交換の寄与が重要な場合には、 ヒッグスの質量 (m_H)、 規格化したトップのヒッグスへの湯川結合定数 (beta_H) で決まる。
そこで問題は、どうやって Gamma あるいは G を測定するかである。 我々はまず、次式で与えられる全断面積を測定できる。
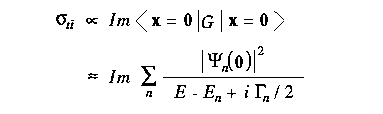
ここで、n の和は、全てのトップオニアム共鳴状態についてとる。 全断面積の測定は、波動関数の原点での値の絶対値のみに 依存することが分かる。
一方、微分断面積（トップの運動量分布）は、運動量空間での 波動関数の形を直接的に反映している。
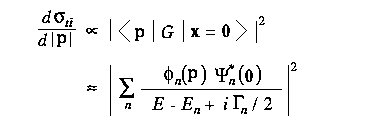
クォークオニアムの波動関数の測定はトップクォークに至って 初めて可能となる点は強調されて良い。 他の軽いクォークオニアムでは、崩壊が対消滅で起こるので、 クォークオニアム中のクォークや反クォークの運動量に関する情報は 失われてしまう。 トップの場合は、トップ崩壊の子供の粒子（b-クォーク、 W の崩壊で出来たクォーク・反クォーク対）の運動量の和として、 親のトップの運動量を測定することが出来る。
まず、しきい値スキャン（しきい値領域での複数のエネルギー点での 全断面積測定）について考えてみよう。 下の図（左）は、しきい値スキャンのモンテカルロ・シミュレーションの 一例である。強い相互作用の結合定数 (alpha_s) の３つの値についての 理論の予想と比較してある。
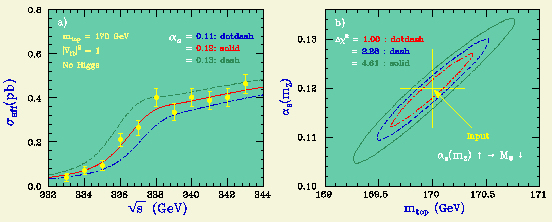
強い相互作用の結合定数が大きくなると、肩の位置（1S 共鳴の名残）が エネルギーの低い方にずれ、またその高さが上がる点に注意する。
右の図は、m_t と alpha_s を自由に動かして、断面積のデーター点を 最小二乗法でフィットした結果である。 m_t と alpha_s の間の強い相関は、alpha_s の増加による 肩の位置の下方へのずれが m_t の増加によって補償出来ることによっている。 この強い相関にもかかわらず、 m_t = 170 GeV の場合、上の例のように 1 fb**-1 の統計の点 11 点を測定すれば、 m_t に対して 0.35 GeV、 alpha_s に対して 0.007 の分解能が期待できる。
エネルギースキャンのデータは、トップの崩壊巾の決定にも利用できる。 トップの崩壊巾が狭くなると、1S 共鳴の名残である肩が高くなり、 一方、裾の部分は低くなる。
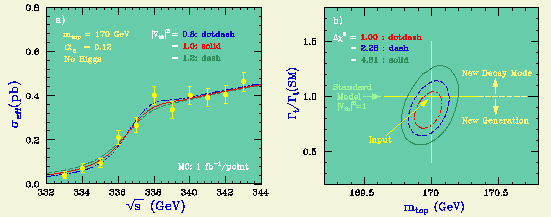
上で m_t と alpha_s を決めるのに使ったのと同じモンテカルロデータを使って、 alpha_s は他の情報から分かっていると仮定すると、m_t および Gamma_t/Gamma_t(SM) をフィットで決められる（上の右の図）。 この場合、トップの崩壊巾に対して期待される統計誤差は、 1 fb**-1 のデータ点 11 点を仮定すると16% である。
同じモンテカルロデータを、ヒッグス質量と 規格化されたトップの湯川結合定数の二乗をパラメーターとして フィットすると下の図を得る。 ただし、モンテカルロにはヒッグス粒子の寄与は入っていない。
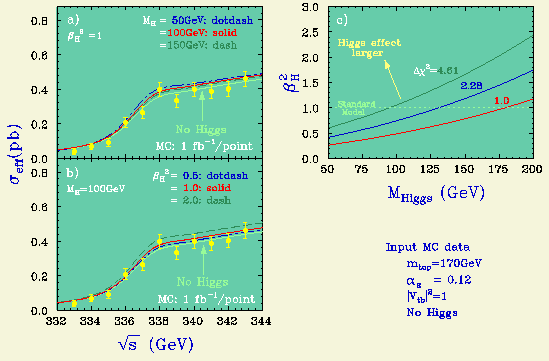
この例は、m_H = 100 GeV の標準理論のヒッグス粒子に対して、 トップの湯川結合定数が 25% の統計精度で計れることを 意味している。
微分断面積測定に進む前に、いろいろなパラメータに対する 期待される統計精度を、m_t = 150, and 170 GeV の場合について、 1 fb**-1 の点 11 点を仮定して、表にまとめておく。
mt (GeV) 150 170
----------------------------------------------
delta m_t (GeV) 0.20 0.35
delta Gamma_t/Gamma_t 0.18 0.16
delta alpha_s(mz) 0.005 0.007
delta Yukawa(mh=100GeV) 0.43 0.25
----------------------------------------------
m_t が増加すると、1S 共鳴がより見にくくなるため、
m_t の精度は悪くなる。
一方、alpha_s や Gamma_t に対する精度は大差ない。
注目すべきは湯川結合に対する感度の向上である。
既に述べたように、微分断面積には、全断面積にはない 情報が含まれている。 まず、トップの運動量分布の形はヒッグス交換の寄与によらない点に 注意しよう。これは、ヒッグス交換の湯川ポテンシャルが 近距離ポテンシャルで、断面積全体にかかるスケール因子としてしか 効かないためである。 この一見不幸な事態は、裏を返せば、運動量分布測定には ヒッグス交換の不定性がないことを意味している。 もう一つ指摘すべき事は、測定点を原理的には観測可能量である 1S 共鳴の位置を基準に固定すれば、運動量分布がトップの質量にも ほとんど依存しなくなる点である。これで、原理的には、 全断面積測定での m_t と alpha_s の強い相関を解くことが出来る。
以下では、運動量測定を 1S 共鳴の 2 GeV 上で行うと仮定する。 alpha_s が増加すると、平均運動量が m_t * alpha_s で与えられるとする ビリアル定理からの素朴な期待に反して、 運動量分布のピークの運動量位置は下がる。 これは、alpha_s が増加すると 1S 共鳴のエネルギーが下がり、 1S を基準に測定エネルーギー点を決めていると、しきい値から測った エネルギーとしては、エネルギーが下がり、その効果で 運動量が下がる効果の方が大きいからである（Jezabek・Kuhun・Teubner）。
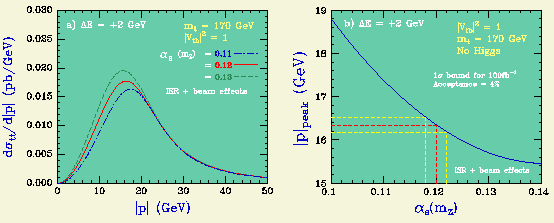
1S 共鳴の位置およびトップの崩壊巾が他の測定から 知られていると仮定すれば、 100 fb**-1 の統計をためるとして、m_t = 170 GeV のトップクォークに対し、 alpha_s の統計精度として 0.0020 が期待できる。
一方、1S 共鳴の位置と alpha_s が他の測定から分かっていれば、 運動量分布から、トップの崩壊巾を決定できる。 運動量分布のピーク位置の運動量は、崩壊幅の増加とともに増大する。 これは、崩壊巾が大きいほど、トップがポテンシャルのより深いところで 崩壊するためである。
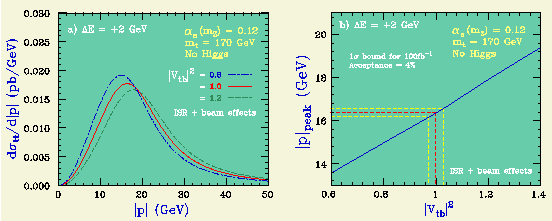
崩壊巾に対する統計精度は、やはり 100 fb**-1 を仮定すれば、 3% である。
しきい値スキャンに対してしたように、運動量測定の いろいろなパラメータに対する感度を表にしておく。 条件は、1S 共鳴の 2 GeV 上で 100 fb**-1 である。
mt (GeV) 150 170
----------------------------------------------
delta Gamma_t/Gamma_t 0.04 0.03
delta alpha_s(mz) 0.0015 0.0020
----------------------------------------------
m_t の差は大してない。
しかし、ここには考慮されていないが、1S 共鳴の位置（E_1S）
の精度は、m_t が大きくなると悪くなることを忘れては成らない。
いずれにせよ、E_1S の誤差は、
しきい値スキャンの統計を上げることにより小さくできる。
一方、全断面積の絶対値の精度は単に統計を上げるだけでは
改善は困難である。
E_1S が与えられれば、形だけが分かればよい運動量測定の利点がここにある。
形の測定は、統計の増加でどんどん改善すると期待できるからである。さて、しきい値領域のトップ・反トップ対生成にはもう一つ新しい特徴がある。 それは前後方非対称度 (A_FB) の測定可能性である（村山・隅野）。 この前後方非対称度は、S-波と P-波の干渉で起こり、 弱い相互作用によって崩壊すること、 大きな崩壊巾によってS-波と P-波が重なり合うことという、 他のオニアムにない トップオニアムにのみ特徴的な性質によっている。 これらに関する詳細は、ライブラリーの PRD50(1994)4341 を参考にされたい。
初めての人にカレンダーライブラリ
JLCホームページへ