Multidimensional Fits in ROOT
Overview
A common problem encountered in different fields of applied science is to find an expression for one physical quantity in terms of several others, which are directly measurable.
An example in high energy physics is the evaluation of the momentum of a charged particle from the observation of its trajectory in a magnetic field. The problem is to relate the momentum of the particle to the observations, which may consists of of positional measurements at intervals along the particle trajectory.
The exact functional relationship between the measured quantities (e.g., the space-points) and the dependent quantity (e.g., the momentum) is in general not known, but one possible way of solving the problem, is to find an expression which reliably approximates the dependence of the momentum on the observations.
This explicit function of the observations can be obtained by a least squares fitting procedure applied to a representive sample of the data, for which the dependent quantity (e.g., momentum) and the independent observations are known. The function can then be used to compute the quantity of interest for new observations of the independent variables.
This class TMultiDimFit implements such a procedure in ROOT. It is largely based on the CERNLIB MUDIFI package [2]. Though the basic concepts are still sound, and therefore kept, a few implementation details have changed, and this class can take advantage of MINUIT [4] to improve the errors of the fitting, thanks to the class TMinuit.
In [5] and [6] H. Wind demonstrates the utility of this procedure in the context of tracking, magnetic field parameterisation, and so on. The outline of the method used in this class is based on Winds discussion, and I refer these two excellents text for more information.
And example of usage is given in $ROOTSYS/tutorials/multidimfit.C.
The Method
Let ![]() by the dependent quantity of interest, which depends smoothly
on the observable quantities
by the dependent quantity of interest, which depends smoothly
on the observable quantities
![]() , which we'll denote by
, which we'll denote by
![]() . Given a training sample of
. Given a training sample of ![]() tuples of the form,
(TMultiDimFit::AddRow)
tuples of the form,
(TMultiDimFit::AddRow)
such that
is minimal. Here
So what TMultiDimFit does, is to determine the number of
terms ![]() , and then
, and then ![]() terms (or functions)
terms (or functions) ![]() , and the
, and the ![]() coefficients
coefficients ![]() , so that
, so that ![]() is minimal
(TMultiDimFit::FindParameterization).
is minimal
(TMultiDimFit::FindParameterization).
Of course it's more than a little unlikely that ![]() will ever become
exact zero as a result of the procedure outlined below. Therefore, the
user is asked to provide a minimum relative error
will ever become
exact zero as a result of the procedure outlined below. Therefore, the
user is asked to provide a minimum relative error ![]() (TMultiDimFit::SetMinRelativeError), and
(TMultiDimFit::SetMinRelativeError), and ![]() will be considered minimized when
will be considered minimized when
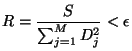
Optionally, the user may impose a functional expression by specifying
the powers of each variable in ![]() specified functions
specified functions
![]() (TMultiDimFit::SetPowers). In that case, only the
coefficients
(TMultiDimFit::SetPowers). In that case, only the
coefficients ![]() is calculated by the class.
is calculated by the class.
Limiting the Number of Terms
As always when dealing with fits, there's a real chance of
over fitting. As is well-known, it's always possible to fit an
![]() polynomial in
polynomial in ![]() to
to ![]() points
points ![]() with
with
![]() , but
the polynomial is not likely to fit new data at all
[1]. Therefore, the user is asked to provide an upper
limit,
, but
the polynomial is not likely to fit new data at all
[1]. Therefore, the user is asked to provide an upper
limit, ![]() to the number of terms in
to the number of terms in ![]() (TMultiDimFit::SetMaxTerms).
(TMultiDimFit::SetMaxTerms).
However, since there's an infinite number of ![]() to choose from, the
user is asked to give the maximum power.
to choose from, the
user is asked to give the maximum power. ![]() , of each variable
, of each variable
![]() to be considered in the minimization of
to be considered in the minimization of ![]() (TMultiDimFit::SetMaxPowers).
(TMultiDimFit::SetMaxPowers).
One way of obtaining values for the maximum power in variable ![]() , is
to perform a regular fit to the dependent quantity
, is
to perform a regular fit to the dependent quantity ![]() , using a
polynomial only in
, using a
polynomial only in ![]() . The maximum power is
. The maximum power is ![]() is then the
power that does not significantly improve the one-dimensional
least-square fit over
is then the
power that does not significantly improve the one-dimensional
least-square fit over ![]() to
to ![]() [5].
[5].
There are still a huge amount of possible choices for ![]() ; in fact
there are
; in fact
there are
![]() possible
choices. Obviously we need to limit this. To this end, the user is
asked to set a power control limit,
possible
choices. Obviously we need to limit this. To this end, the user is
asked to set a power control limit, ![]() (TMultiDimFit::SetPowerLimit), and a function
(TMultiDimFit::SetPowerLimit), and a function
![]() is only accepted if
is only accepted if
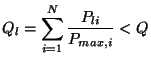
Gram-Schmidt Orthogonalisation
To further reduce the number of functions in the final expression,
only those functions that significantly reduce ![]() is chosen. What
`significant' means, is chosen by the user, and will be
discussed below (see 2.3).
is chosen. What
`significant' means, is chosen by the user, and will be
discussed below (see 2.3).
The functions ![]() are generally not orthogonal, which means one will
have to evaluate all possible
are generally not orthogonal, which means one will
have to evaluate all possible ![]() 's over all data-points before
finding the most significant [1]. We can, however, do
better then that. By applying the modified Gram-Schmidt
orthogonalisation algorithm [5] [3] to the
functions
's over all data-points before
finding the most significant [1]. We can, however, do
better then that. By applying the modified Gram-Schmidt
orthogonalisation algorithm [5] [3] to the
functions ![]() , we can evaluate the contribution to the reduction of
, we can evaluate the contribution to the reduction of
![]() from each function in turn, and we may delay the actual inversion
of the curvature-matrix
(TMultiDimFit::MakeGramSchmidt).
from each function in turn, and we may delay the actual inversion
of the curvature-matrix
(TMultiDimFit::MakeGramSchmidt).
So we are let to consider an ![]() matrix
matrix
![]() , an
element of which is given by
, an
element of which is given by
where
and
We now take as a new model
![]() . We thus want to
minimize
. We thus want to
minimize
where
or
Let
Using (9), we see that
So for each new function ![]() included in the model, we get a
reduction of the sum of squares of residuals of
included in the model, we get a
reduction of the sum of squares of residuals of
![]() ,
where
,
where
![]() is given by (4) and
is given by (4) and ![]() by
(9). Thus, using the Gram-Schmidt orthogonalisation, we
can decide if we want to include this function in the final model,
before the matrix inversion.
by
(9). Thus, using the Gram-Schmidt orthogonalisation, we
can decide if we want to include this function in the final model,
before the matrix inversion.
Function Selection Based on Residual
Supposing that ![]() steps of the procedure have been performed, the
problem now is to consider the
steps of the procedure have been performed, the
problem now is to consider the
![]() function.
function.
The sum of squares of residuals can be written as
where the relation (9) have been taken into account. The contribution of the
Two test are now applied to decide whether this
![]() function is to be included in the final expression, or not.
function is to be included in the final expression, or not.
Test 1
Denoting by ![]() the subspace spanned by
the subspace spanned by
![]() the function
the function
![]() is
by construction (see (4)) the projection of the function
is
by construction (see (4)) the projection of the function
![]() onto the direction perpendicular to
onto the direction perpendicular to ![]() . Now, if the
length of
. Now, if the
length of
![]() (given by
(given by
![]() )
is very small compared to the length of
)
is very small compared to the length of
![]() this new
function can not contribute much to the reduction of the sum of
squares of residuals. The test consists then in calculating the angle
this new
function can not contribute much to the reduction of the sum of
squares of residuals. The test consists then in calculating the angle
![]() between the two vectors
between the two vectors
![]() and
and
![]() (see also figure 1) and requiring that it's
greater then a threshold value which the user must set
(TMultiDimFit::SetMinAngle).
(see also figure 1) and requiring that it's
greater then a threshold value which the user must set
(TMultiDimFit::SetMinAngle).
Test 2
Let
![]() be the data vector to be fitted. As illustrated in
figure 1, the
be the data vector to be fitted. As illustrated in
figure 1, the
![]() function
function
![]() will contribute significantly to the reduction of
will contribute significantly to the reduction of ![]() , if the angle
, if the angle
![]() between
between
![]() and
and
![]() is smaller than
an upper limit
is smaller than
an upper limit ![]() , defined by the user
(TMultiDimFit::SetMaxAngle)
, defined by the user
(TMultiDimFit::SetMaxAngle)
However, the method automatically readjusts the value of this angle
while fitting is in progress, in order to make the selection criteria
less and less difficult to be fulfilled. The result is that the
functions contributing most to the reduction of ![]() are chosen first
(TMultiDimFit::TestFunction).
are chosen first
(TMultiDimFit::TestFunction).
In case ![]() isn't defined, an alternative method of
performing this second test is used: The
isn't defined, an alternative method of
performing this second test is used: The
![]() function
function
![]() is accepted if (refer also to equation (13))
is accepted if (refer also to equation (13))
where
From this we see, that by restricting ![]() -- the number of
terms in the final model -- the fit is more difficult to perform,
since the above selection criteria is more limiting.
-- the number of
terms in the final model -- the fit is more difficult to perform,
since the above selection criteria is more limiting.
The more coefficients we evaluate, the more the sum of squares of
residuals ![]() will be reduced. We can evaluate
will be reduced. We can evaluate ![]() before inverting
before inverting
![]() as shown below.
as shown below.
Coefficients and Coefficient Errors
Having found a parameterization, that is the ![]() 's and
's and ![]() , that
minimizes
, that
minimizes ![]() , we still need to determine the coefficients
, we still need to determine the coefficients
![]() . However, it's a feature of how we choose the significant
functions, that the evaluation of the
. However, it's a feature of how we choose the significant
functions, that the evaluation of the ![]() 's becomes trivial
[5]. To derive
's becomes trivial
[5]. To derive
![]() , we first note that
equation (4) can be written as
, we first note that
equation (4) can be written as
where
Consequently,
The model
The reason we use
Considerations
It's important to realize that the training sample should be representive of the problem at hand, in particular along the borders of the region of interest. This is because the algorithm presented here, is a interpolation, rahter then a extrapolation [5].
Also, the independent variables ![]() need to be linear
independent, since the procedure will perform poorly if they are not
[5]. One can find an linear transformation from ones
original variables
need to be linear
independent, since the procedure will perform poorly if they are not
[5]. One can find an linear transformation from ones
original variables ![]() to a set of linear independent variables
to a set of linear independent variables
![]() , using a Principal Components Analysis
(see TPrincipal), and
then use the transformed variable as input to this class [5]
[6].
, using a Principal Components Analysis
(see TPrincipal), and
then use the transformed variable as input to this class [5]
[6].
H. Wind also outlines a method for parameterising a multidimensional dependence over a multidimensional set of variables. An example of the method from [5], is a follows (please refer to [5] for a full discussion):
- Define
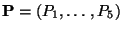 are the 5 dependent
quantities that define a track.
are the 5 dependent
quantities that define a track.
- Compute, for
 different values of
different values of
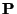 , the tracks
through the magnetic field, and determine the corresponding
, the tracks
through the magnetic field, and determine the corresponding
 .
.
- Use the simulated observations to determine, with a simple
approximation, the values of
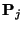 . We call these values
. We call these values
 .
.
- Determine from
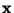 a set of at least five relevant
coordinates
a set of at least five relevant
coordinates
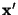 , using contrains, or
alternative:
, using contrains, or
alternative:
- Perform a Principal Component Analysis (using
TPrincipal), and use
to get a linear transformation
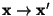 , so that
, so that
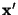 are constrained and linear independent.
are constrained and linear independent.
- Perform a Principal Component Analysis on
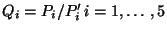 , to get linear
indenpendent (among themselves, but not independent of
, to get linear
indenpendent (among themselves, but not independent of
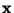 ) quantities
) quantities
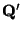
- For each component
 make a mutlidimensional fit,
using
make a mutlidimensional fit,
using
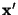 as the variables, thus determing a set of
coefficents
as the variables, thus determing a set of
coefficents
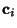 .
.
To process data, using this parameterisation, do
- Test wether the observation
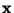 within the domain of
the parameterization, using the result from the Principal Component
Analysis.
within the domain of
the parameterization, using the result from the Principal Component
Analysis.
- Determine
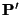 as before.
as before.
- Detetmine
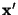 as before.
as before.
- Use the result of the fit to determind
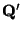 .
.
- Transform back to
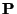 from
from
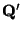 , using
the result from the Principal Component Analysis.
, using
the result from the Principal Component Analysis.
Testing the parameterization
The class also provides functionality for testing the, over the
training sample, found parameterization
(TMultiDimFit::Fit). This is done by passing
the class a test sample of ![]() tuples of the form
tuples of the form
![]() , where
, where
![]() are the independent
variables,
are the independent
variables, ![]() the known, dependent quantity, and
the known, dependent quantity, and ![]() is
the square error in
is
the square error in ![]() (TMultiDimFit::AddTestRow).
(TMultiDimFit::AddTestRow).
The parameterization is then evaluated at every
![]() in the
test sample, and
in the
test sample, and

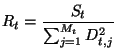
It's possible to use Minuit [4] to further improve the fit, using the test sample.
November 2000, NBI

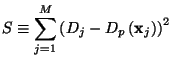
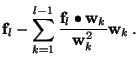
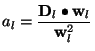
![$\displaystyle S_l = \left[\mathbf{D} - \sum^l_{k=1} a_k\mathbf{w}_k\right]^2 = ...
...2 - 2\mathbf{D} \sum^l_{k=1} a_k\mathbf{w}_k + \sum^l_{k=1} a_k^2\mathbf{w}_k^2$](gif/multidimfit_img70.gif)
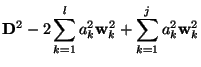
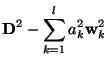
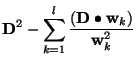
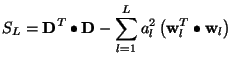

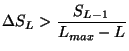

![$\displaystyle \mathbf{c} = \left(\mathsf{B}^{-1}\mathbf{a}\right) = \left[\mathbf{a}^T\left(\mathsf{B}^{-1}\right)^T\right]^T .$](gif/multidimfit_img97.gif)