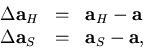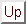

Next: Vertex Fitting
Up: Track Linking
Previous: Helix to Helix
Given a straight line track and a helical track, we can combine them to
improve the helix parameter measurements as we did for the helix
to helix linking![[*]](foot_motif.gif) .
Again the pivots should be chosen at a common space point:
the best choice is the intersection of the straight line track with
the boundary of the two regions.
We then correct the error matrix of the straight line track for
multiple scattering.
Then the
.
Again the pivots should be chosen at a common space point:
the best choice is the intersection of the straight line track with
the boundary of the two regions.
We then correct the error matrix of the straight line track for
multiple scattering.
Then the 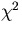 to minimize is defined by
to minimize is defined by
| 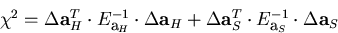 |
(24) |
with
where
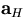 and
and 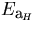 are the helix parameter vector and
its error matrix, while
are the helix parameter vector and
its error matrix, while
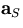 and
and 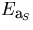 are derived from those of
the straight line (
are derived from those of
the straight line (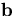 and
and
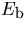 ) as follows
) as follows![[*]](foot_motif.gif) :
:
| 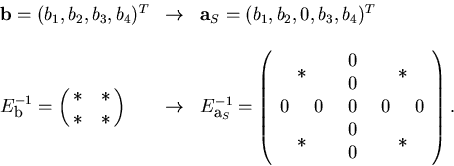 |
(25) |
Then what follows is the same as with the helix to helix linking in the
previous subsection:
it reduces to the two-track case: i = H, S in
Eq.2.5.31![[*]](foot_motif.gif) .
.
Keisuke Fujii
12/4/1998
![[*]](foot_motif.gif) .
Again the pivots should be chosen at a common space point:
the best choice is the intersection of the straight line track with
the boundary of the two regions.
We then correct the error matrix of the straight line track for
multiple scattering.
Then the
.
Again the pivots should be chosen at a common space point:
the best choice is the intersection of the straight line track with
the boundary of the two regions.
We then correct the error matrix of the straight line track for
multiple scattering.
Then the