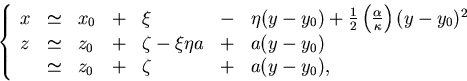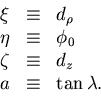

Next: Track Fitting in r-
Up: High Momentum Limit
Previous: High Momentum Limit
We consider a high momentum
track originating from the interaction point (IP) region.
When we take our local coordinate system in such a way that
the z axis is along the magnetic field, the y axis in the radial
direction which is approximately along the transverse momentum of the track,
and the x axis makes the overall system right-handed,
the helical track can be approximated by![[*]](foot_motif.gif)
| 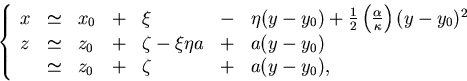 |
(41) |
where we have introduced the following short-hand for the
helix parameters:
Notice that the last approximation (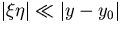 ),
which is justified by our choice of the coordinate system
(
),
which is justified by our choice of the coordinate system
(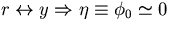 ),
makes the r-
),
makes the r-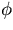 and the r-z fittings decouple from each other.
We will, thus, the r-
and the r-z fittings decouple from each other.
We will, thus, the r-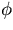 and the r-z fittings separately
in what follows.
Notice also that the problem then becomes a linear one, which
simplifies the necessary calculations considerably.
and the r-z fittings separately
in what follows.
Notice also that the problem then becomes a linear one, which
simplifies the necessary calculations considerably.
Keisuke Fujii
12/4/1998
![[*]](foot_motif.gif)
![[*]](foot_motif.gif)