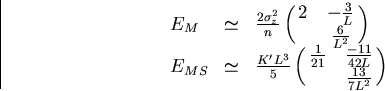

Next: Examples of Applications
Up: Track Fitting in r-z
Previous: Pivot Transformation
Now let us turn our attention to the r-z track fitting under
the influence of multiple scattering.
The treatment here provides a way to calculate the E0
of the last subsection including
multiple scattering effects in track fitting.
From now on, we take (y0,z0) = (0,0) and 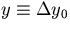 .The multiple scattering modifies the track parameter of the particle as
.The multiple scattering modifies the track parameter of the particle as
| 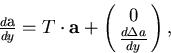 |
(90) |
where
| 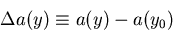 |
(91) |
represents the change of the dip angle due to the multiple
scattering as a function of y.
This results in
| 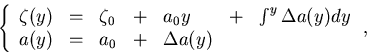 |
(92) |
where the parmeters with the suffix are those at the
initial point before multiple scattering.
Now, let us assume that we are given
(n+1) hit points, 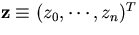 ,measured at fixed y positions,
,measured at fixed y positions, 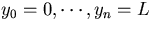 .Then the minimization of the
.Then the minimization of the 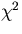 :
:
| 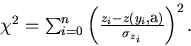 |
(93) |
The parameter vector that gives the 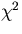 minimum is
minimum is
| 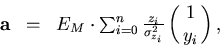 |
(94) |
with
| 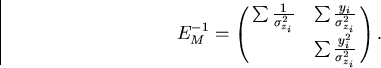 |
(95) |
Through the above equation, the change in 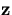 due to the multiple scattering induces a change in
due to the multiple scattering induces a change in 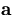 :
:
| 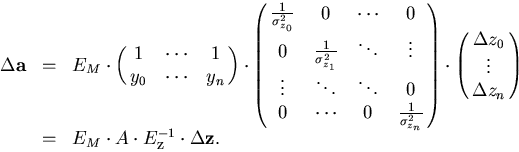 |
(96) |
From this we obtain the full error matrix including multiple scattering:
| 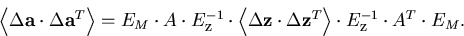 |
(97) |
Again the problem reduces to the evaluation of the
correlation matrix in the coordinate measurements:
| 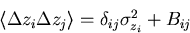 |
(98) |
with
| ![\begin{displaymath}
\begin{array}
{lll}
B_{ij} & \equiv & N' \int [d\Delta a] ~...
...ght) \cr
& = & \frac{K'}{2} y_i^2 ( y_j - y_i/3 ) ,\end{array}\end{displaymath}](img222.gif) |
(99) |
where the last expression is valid for 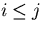 .The full error matrix is then written in the form:
.The full error matrix is then written in the form:
| 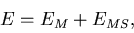 |
(100) |
where the first term is from the coordinate measurement errors while the
second term from the multiple scattering:
| 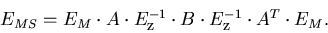 |
(101) |
In the case of equal space sampling with the same position resolution,
EM and EMS reduce to
| 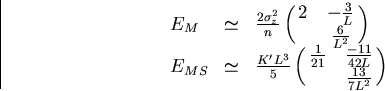 |
(102) |
with
| 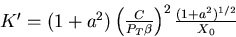 |
(103) |
in the large n limit.


Next: Examples of Applications
Up: Track Fitting in r-z
Previous: Pivot Transformation
Keisuke Fujii
12/4/1998
![]() .The multiple scattering modifies the track parameter of the particle as
.The multiple scattering modifies the track parameter of the particle as
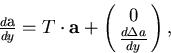
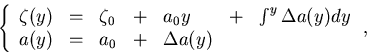
![]() ,measured at fixed y positions,
,measured at fixed y positions, ![]() .Then the minimization of the
.Then the minimization of the ![]() :
:
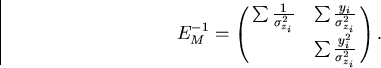
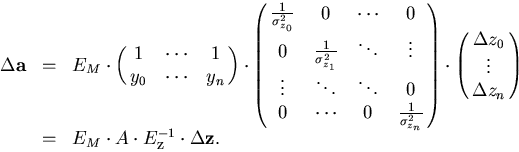
![\begin{displaymath}
\begin{array}
{lll}
B_{ij} & \equiv & N' \int [d\Delta a] ~...
...ght) \cr
& = & \frac{K'}{2} y_i^2 ( y_j - y_i/3 ) ,\end{array}\end{displaymath}](img222.gif)